Watch the Khan Academy video “Trapezoidal Approximation” and learn how it
relates to work done on a gas.
Use the Observe Pressure Sensor to collect pressure data in the Desmos Graphing
Calculator as you do work to decrease the volume of a syringe.
Construct trapezoids in Desmos to estimate the area under your pressure-volume (PV) curve.
Convert the sum of trapezoid areas to determine the total work done on the gas during
compression, expressed in Joules.
Getting Ready:
Gas particles: tiny molecules moving in constant, random motion.
Pressure: the force created by gas particles striking the walls of a container.
Volume: the amount of space available for those particles to move around in.
Work: when you press the syringe plunger inward, you apply a force and the
plunger moves. Work is defined as a force acting over a distance.
Area under the PV curve: the force needed to push the plunger is not constant—
it increases as the gas is compressed. On a pressure–volume graph, the area under
the curve represents the total work done on the gas.
Click to watch this Khan Academy video to learn more about these concepts.
×
Click this link
Work Done on a Gas Worksheet
to open the worksheet. If your class uses Google Classroom,
open the worksheet from your assignment. If not, click the
link above, choose Make a copy, complete your work, and
turn it in the usual way.
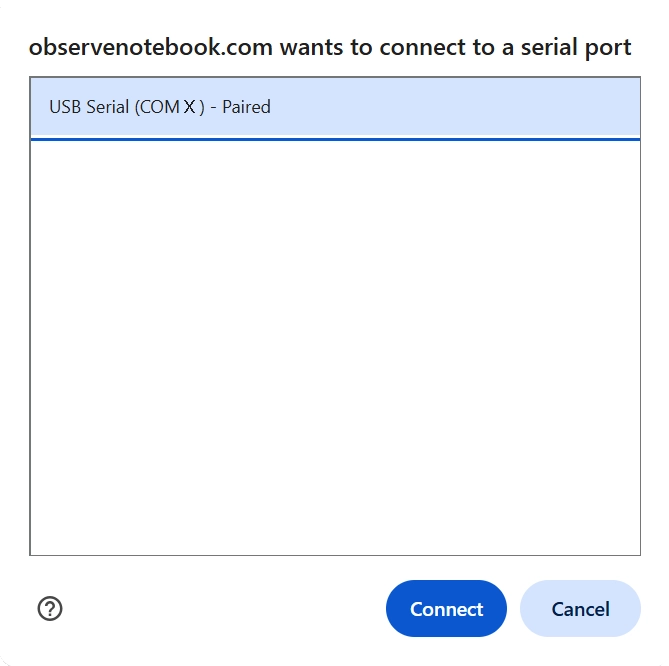
Click the Show Directions button in the upper-right
corner to learn how to collect data for this activity.
What Do You Think?
Imagine the area under the curve below divided into four trapezoids, each with
a width of 1 along the x-axis. Do you see how adding the areas of these
trapezoids provides an approximation of the true area under the curve?
Use your mouse to click and drag on the graph below to draw four equal-width
trapezoids under the curve. If you need to start over, click
Erase Drawing. When you are satisfied, click
Capture Drawing to copy the image to the clipboard and paste it
into your worksheet for this activity.
Directions:
Use a USB-C cable to plug the Observe pressure sensor
into your computer's USB port.
Click the Connect Sensor button to activate the
sensor.
Select the USB serial port (COM X). The X value varies by
computer and is not important. Then click the blue Connect
button in the pop-up window. The status will change to
ready.
Adjust the plunger of the syringe to exactly 20 mL and attach
the syringe to your pressure sensor. Notice the pressure reading in
units of kilopascals (kPa) above the graph. Pressing the plunger down
to reduce the volume causes the pressure to increase.
Add measurements one at a time by pressing the Add
Point button. When pressed, you are prompted for the
x-value for the corresponding y measurement. Your first point should
be 20 mL. Next, reduce the volume to 19 mL and add another point. Continue
reducing the volume by 1 mL and adding points until a volume of 5 mL.
Clear Graph resets; Capture Graph copies an
image of the graph to the clipboard; Export/Import saves or opens a CSV data file.
Click the small gray triangle to the left of the data table
to view the sensor data (V, P, and A) in the table.
Click the Show Instructions button in the upper right
to continue with analysis of the data.
Data Collection
(0, —)Analyzing Your Data:
Click the
button to apply the trapezoid rule. The area of each trapezoid will appear in
column A (kPa·mL) of the data table.
Find the total approximate area under the PV curve. Enter the equation (use the underscore key _ to make the subscript) below in the Desmos expression window.
Convert your trapezoid sum from kPa·mL to Joules by rewriting the units in SI form:
1 kPa = 1,000 Pa and 1 mL = 1×10⁻⁶ m³. Since
1 kPa·mL = 1×10⁻³ J, multiply your result by 0.001
(because 1,000 × 1×10⁻⁶ = 1×10⁻³) to obtain the work in Joules. Multiply the total area by .001 in the Desmos expression window.
Calculate an accepted value by evaluating the definite integral from 4 mL to 20 mL
using Boyle’s Law for an isothermal compression and compare this exact value
with your trapezoid-rule approximation for the same interval. Enter the equation below in the Desmos expression window.
Going Further:
Try
Boyle’s Law: Pressure–Volume
to explore mathematical modeling of the relationship between the pressure and
volume of a gas.
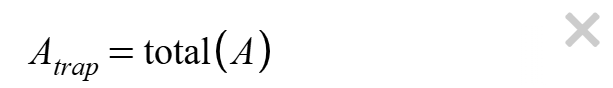
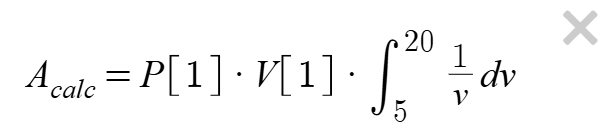Going Further: